Financial Literacy

Unit 2 – Time Value of Money

Lesson 2.3: What is Interest?

Anytime a lender lends money to a borrower, they do so with agreement that the amount lent will be repaid by borrower along with additional money to compensate the lender for the following:

• Risk lender took on in providing the money to the borrower; and,
• The time that the lender was unable to utilize this money in other ways (Opportunity Cost)

 

Interest is simply the cost of borrowing money. 

In this lesson, we will be focusing on the interest experienced through lending; however, the same concepts can be applied to wealth accumulation.  It is no different when you place your money in a Savings Account that offers interest.  In this situation, you simply take over the role of the lender and the bank providing the interest becomes the borrower.  Due to this, in all our lifetimes we will be subjected to this lender-borrower agreement, and as such, interest will influence all of our finances. 

We are going to be focusing on the two types of Interest: Simple Interest and Compound Interest.

• Simple Interest:

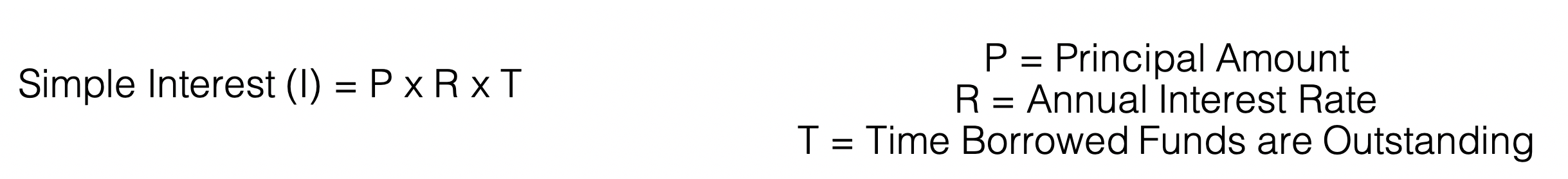
Simple Interest is the interest generated on the original principal amount of any loan. The formula used to calculate Simple Interest is:

Example – Simple Interest:

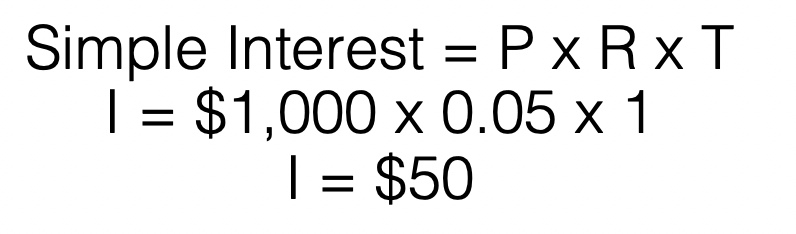
You borrow $1,000 from a bank at a Simple Interest Rate of 5%, with no payments due until the end of a 10-Year period.  The bank calculates the amount of money you will owe in interest at the end of each year using the following formula:

If this continues over the course of 10 years, you can expect the following:

 

Compound Interest:

In contrast, Compound Interest is calculated on the sum of the principal amount and the interest that accumulates each period. This is the reason why Compound Interest is often referred to as ‘interest on interest’. 

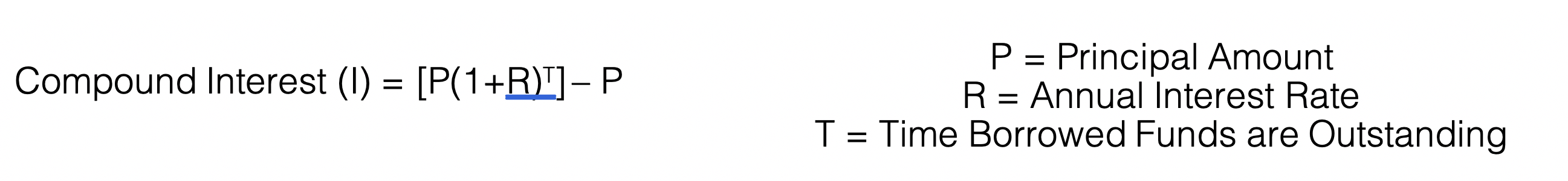
Compound Interest over long periods of time can increase the initial principal amount dramatically. It is beneficial with investing; however, it is something to consider when you are paying back a loan as the effects are equally as powerful when borrowing money.

Example – Compound Interest:
Here we are using the same bank loan example from earlier. The only difference is that unlike last time, the agreement that you have with the bank now includes a Compounding Interest Rate of 5%. 

In this case, we can expect the following:

 

Comparison: Simple Interest vs. Compound Interest

You can see the effects Compound Interest have in comparison to Simple Interest.  When it comes to situations in which there is money borrowed, Compound Interest provides a larger overall debt, at the end of the timeframe, than in the case of Simple Interest.  Moreover, in the case of the Compound Interest the growth of the Total Amount Owed is experiencing what is considered Exponential Growth.

Exponential Growth is the phenomenon whereby the increases in growth year-by-year increases over time.  In the example above, this is captured by the increases we see in the Annual Interest experienced.  In the first example of Simple Interest this figure remains constant at $50 each year.  In the Compound Interest example, this figure not only rises, but it is rising by a larger and larger amount each year, until Year 10, where the $77.57 is a total $27.57 more than what was seen in Year 1. 

Example – Simple Interest vs. Compound Interest:
The effects of Simple Interest and Compound Interest are not restricted to the arena of loans.  The same principles can be seen in the form of investments as well.  In the example below, we are comparing two people who invest the same amount of money, at the same time, into the same investment.  The only difference between the two is one person withdraws their gain each year (their interest earned) and the other leaves the interest in the investment for the entire time. 

In this example, the person who withdraws each year will experience investment growth in the form of Simple Interest, while the person who does not withdraw will experience Compound

Interest growth.

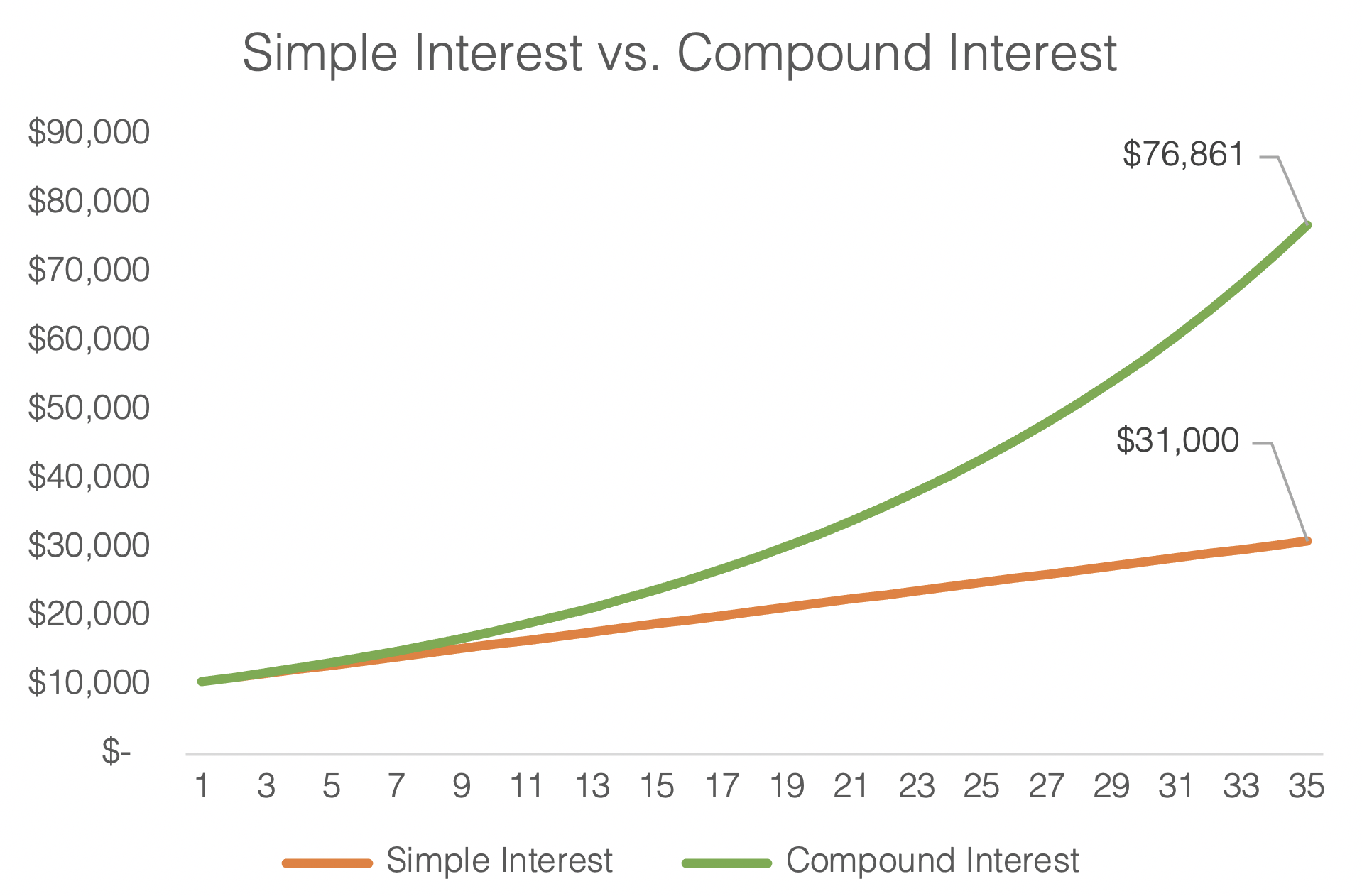
This scenario will highlight the significance that Exponential Growth can play on your finances. 
The graph above shows the difference between Compound Interest and Simple Interest investments of $10,000, with an Interest Rate of 6%, over 35 years.

Summary

Time plays such a huge role in the effect of Compounding Interest.  Although both investors in our example experience the same return in Year 1 (prior to any interest being compounded), their annual interest returns become incrementally different as the years pass, to the point that the difference in total return over the 35-year period, amounts to a whopping $45,861.  This is another reason why delaying one’s own financial planning may not seem like a substantial decision in the present but can have a huge impact on your finances in the future. 

Being familiar with the distinction between Simple Interest and Compound Interest is crucial as we expand upon this knowledge in the remainder of Unit 2 and beyond. In Lesson 2.4, we will discuss other ways in which we distinguish Interest Rates, mainly how we can incorporate Inflation.